Understanding Quadrilaterals in Geometry

Key Terms

o Quadrilateral

o Simple quadrilateral

o Complex quadrilateral

o Concave quadrilateral

o Convex quadrilateral

o Trapezoid

o Isosceles trapezoid

o Parallelogram

o Rectangle

o Square

Objectives

o Know the basic properties of quadrilaterals

o Recognize specific classes of quadrilaterals and their characteristics

o Calculate the area of certain special quadrilaterals

A quadrilateral is a figure with four sides; common examples of quadrilaterals include squares, rectangles, and trapezoids. Quadrilaterals break down into several categories: simple quadrilaterals are those that do not have any self-crossings (in the manner of the bowtie shape below, for example); complex quadrilaterals do have self-crossings. Examples are shown below.

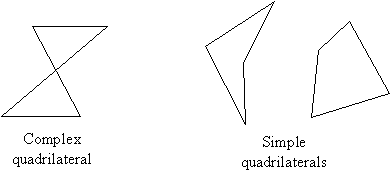
In the class of simple quadrilaterals are concave quadrilaterals (such as the leftmost simple quadrilateral above) and convex quadrilaterals. A concave quadrilateral contains a reflex angle (an angle greater than 180°), whereas all of the angles in a convex quadrilateral are less than 180°. Again, the examples in the diagram above illustrate these characteristics. In our discussion, we will only consider simple convex quadrilaterals--these include such figures as rectangles.

In addition to having four sides, quadrilaterals also have four vertices and four interior angles. One particular property of quadrilaterals that we can immediately derive is the total number of degrees in the sum of interior angles. Recall that our study of triangles showed that every triangle has 180° (that is, the measures of the interior angles always sum to 180°). We can use this fact about triangles to determine the sum of the angles in a quadrilateral. Consider the generic quadrilateral below; we can draw a diagonal line between two non-adjacent vertices to form two triangles.

Thus, if we add up all the measures of the interior angles in the two triangles, we then know how many degrees are in a quadrilateral. Of course, this sum is twice 180°, or a total of 360°. This result makes sense if you already know that a rectangle contains four right angles!

Types of Quadrilaterals--Trapezoids

Certain types of quadrilaterals have properties that allow us to derive expressions and other information about them. For instance, a quadrilateral with either one or two pairs of parallel opposite sides have special characteristics that we can study further. A quadrilateral with one pair of parallel opposite sides is called a trapezoid. (We will only consider a trapezoid to be a quadrilateral with exactly one pair of parallel opposite sides--thus, a quadrilateral with two pairs of parallel opposite sides is not a trapezoid by our definition.) A diagram of a generic trapezoid is shown below.

A special type of trapezoid is the so-called isosceles trapezoid, which has two non-parallel sides of equal length.

Let's derive a general formula for the area; we can use what we know about triangles as well as the area of a rectangle (which is the product of the length and width). First, we'll divide the trapezoid into two triangles and a rectangle, as shown below, where the dashed lines are both perpendicular to the parallel sides. The lengths of the parallel sides are b₁ and b₂.

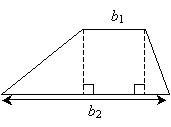
Notice that we can break down the length b₂ into the sum of three different line segments: the base of the triangle on the left (which we'll call x), the width of the rectangle (which is equal to b₁), and the base of the triangle on the right (which we'll call y). On the basis of these definitions, we know that b₂ is equal to x + y + b₁. Furthermore, let's call the lengths of the dashed lines h, since they represent the height of the trapezoid.

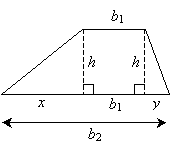
Now, the trapezoid is divided into three figures whose areas we know how to calculate. Let's call the area of the trapezoid A; we can then derive a formula as follows.

Let's divide the middle term in half so that we can simplify the expression.

But we know from our definition that x + b₁ + y is simply b₂.

Thus, we have derived a simple formula for the area of a trapezoid with height h and parallel sides of lengths b₁ and b₂.

Types of Quadrilaterals--Parallelograms

If a quadrilateral has two pairs of parallel opposite sides, then it is called a parallelogram. Parallel sides in a parallelogram are also congruent in length. In addition, because opposite sides are parallel, opposite angles are congruent as well. An example of a parallelogram, with congruent parts identified, is shown below.

As with the trapezoid, we can derive a formula for the area of a parallelogram by dividing it into a rectangle and two triangles.

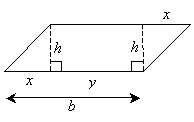
Want to learn more? Take an online course in Geometry.

Notice that we have labeled the dashed lines with the length h (for the height of the parallelogram) and the upper and lower parallel sides with length b (for the base of the parallelogram). We have also divided the base into length x (the base of the triangle) and length y (the width of the rectangle). Notice that the two triangles are right triangles and that we can prove they are congruent by the SAS (side-angle-side) condition. Thus, the total area in the two triangles is simply xh. We know that the area of the rectangle is yh, so the total area A of the parallelogram is the following:

But x + y is simply b; thus the area is

A = bh

Notice that if any angle in the parallelogram is a right angle, the parallelogram becomes a rectangle (opposite angles are congruent, and there are a total of 360° in a parallelogram-thus, if one angle in a parallelogram is a right angle, they must all be right angles).

As we have mentioned several times previously, the area of a rectangle is simply the product of its length (height) and width (base). This fact is easy to see through an example.

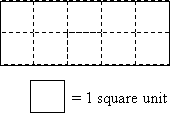
The area is obviously 10 square units, since it takes 10 of the squares to fill the entire rectangle. Note, however, that we can also view the area as 2 rows of 5 squares each, and the product of 2 and 5 is 10. Thus, as mentioned, the area of a rectangle is simply the product of the length and width (or height and base, using parallelogram terms).

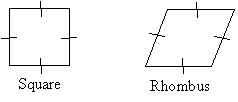
If a rectangle has all four sides of equal length (in other words, adjacent sides are congruent), then the rectangle is called a square. A square has four congruent sides as well as four congruent angles. More generally, any parallelogram with four sides of equal length is called a rhombus. A square and rhombus are shown below.

We can draw a tree diagram that shows the relationships of the various simple convex quadrilaterals that we have discussed.

Practice Problem: A kite is a quadrilateral with two pairs of non-opposite congruent sides, as shown below. Determine the area of the kite using the information provided in the diagram.

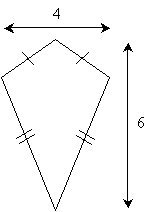
Solution: Let's start by dividing the kite into two isosceles triangles.

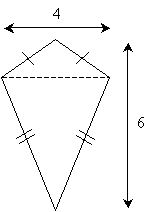
Note that we now know the base of these two triangles: the given length of 4 units. The combined height of the two isosceles triangles is 6 units; we do not know the exact value of each individual height, however. Nevertheless, we can assign variables x and y to these heights, as shown below, while noting that x + y is 6 units.

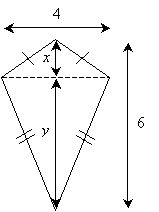
Since we know how to calculate the area of a triangle, we can calculate the area of the kite by adding the areas of the two triangles.

Thus, the area of the kite is 12 square units.

Practice Problem: Find the length of the diagonal of a square (a diagonal is a line segment connecting opposite vertices) with sides of length x.

Solution: Let's start by drawing a diagram of a square and one of its two diagonals.

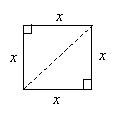
The diagonal divides the square into two congruent (by the SAS condition) right triangles. Notice that the two triangles share the same hypotenuse, which is the diagonal of the square. We can calculate the length of the diagonal (which we'll call h) using the Pythagorean theorem.

Thus, using the properties of squares and triangles, we have been able to determine a general formula for the length of a diagonal in a square.

Practice Problem: Determine if the following quadrilateral is a parallelogram.

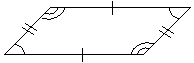
Solution: Recall that a parallelogram has congruent opposite sides and congruent opposite angles. We can take any of several possible approaches to this problem. One possible approach is to prove that the triangles created by the diagonal (dashed) line are congruent-we can show this by the ASA (angle-side-angle) condition, since both triangles share the same diagonal as the included side. As a result, given the orientation of the triangles, opposite sides of the quadrilateral are congruent, which implies that the quadrilateral is a parallelogram. Another approach is to show that both pairs of opposite sides are parallel. Recall that when a transversal (such as the diagonal above) cuts two parallel lines, corresponding angles are congruent. Thus, the top and bottom sides of the quadrilateral are parallel because the angles marked by a single arc are congruent, and the left and right sides of the quadrilateral are parallel because the angles marked by double arcs are likewise congruent. These are but two possible approaches to solving this problem.