Key Terms
o Transformation
o Translation
o Reflection
o Line of reflection
o Rotation
o Center of rotation
o Dilation
o Angle-angle condition
o Side-side-side (proportionality) condition
o Side-angle-side (proportionality) condition
Objectives
o Understand how transformations can be used as a method of understanding congruence and similarity
o Prove that two triangles are similar using appropriate criteria
Another View of Congruence and Similarity
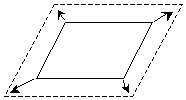
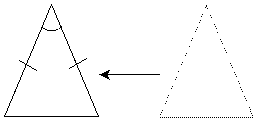
Let's review the task of proving that two triangles are similar. Recall that congruence means that the measures of all three sides and all three angles are the same for the two triangles. For similarity, all that is required is that the angles be congruent. Another way of looking at congruence and similarity is by way of geometric transformations. A transformation, in layman's terms, is simply a movement or change in the figure. Four basic transformations are translations, reflections, rotations, and dilations. A translation is simply a movement of the entire figure across some distance, where the shape and orientation of the figure remain unchanged. A translation is shown below.
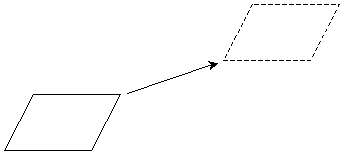
Another transformation is a reflection, which produces a mirror image of the figure. A line of reflection must be chosen to serve as the "mirror" for producing the reflected figure. A reflection is shown below.
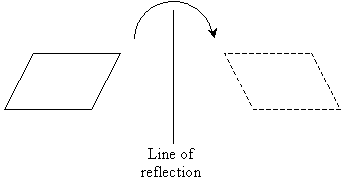
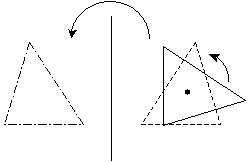
A rotation, as the name indicates, simply involves "spinning" the figure around some point (this center of rotation can be either inside or outside the figure). Two rotations are shown below: the leftmost example has a center of rotation inside the figure, and the rightmost example has a center of rotation outside the figure.
Finally, a dilation is simply an expansion or reduction of the figure such that the new figure is proportional in all its dimensions.
If two figures are congruent, then one figure can be superimposed onto the other by way of some combination of translations, reflections, and rotations. Consider the two congruent triangles below.
If we rotate the triangle on the right by a quarter turn (in the counterclockwise direction) and then reflect it, the result is a triangle that perfectly matches the triangle on the left.
These mathematical manipulations are a more rigorous way of saying that if we cut out of a piece of paper two triangles with exactly the same shape, then those triangles are still the same no matter how we turn, flip, or move those pieces of paper!
If the two triangles (or other figures) can be imposed through some series of transformations that includes a dilation, then the triangles are similar. Consider the two similar triangles shown below.
By dilating and translating the smaller triangle, we can create a perfect overlap on the larger triangle. Because a dilation is necessary, these triangles are similar but not congruent.
Practice Problem: Determine a series of transformations that shows the triangles below to be congruent.
Solution: To demonstrate that the two triangles above are congruent, we need to perform a series of transformations (translations, rotations, or reflections) such that one triangle perfectly overlaps another. Let's perform our transformations on the right-hand triangle. By inspection, we see that we need to rotate the triangle (180°) and then translate it leftward.
Again, because the triangles overlap, they are congruent (we also know the triangles are congruent from the given diagram by the SAS condition).
Practice Problem: Show by some series of transformations that the triangles below are similar.
Solution: If we can find a series of geometric transformations (translations, rotations, reflections, or dilations) that allows us to make the triangle on the right overlap that on the left, then the triangles are similar. By the side-angle-side (proportionality) condition, we can already see that the triangles are similar. To make them congruent, let's first dilate the triangle on the right (that is, we'll expand it to three times its current size).
Next, we'll translate the triangle to the left to show the perfect overlap, thus demonstrating that the triangles are similar.
Proving Similarity
As with congruence, we can identify several conditions for proving similarity in triangles that does not require us to show that all three angles are congruent. Again, the condition for similarity is that the interior angles of one triangle are congruent with those of another triangle.
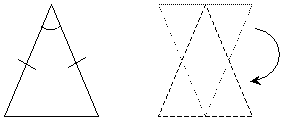
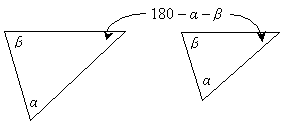
The first condition that we can use to prove similarity is the angle-angle condition. Recall that the sum of all the angles in a triangle is always 180°; thus, if two triangles have two angles that are congruent, they must also have a third angle that is congruent, as shown below.
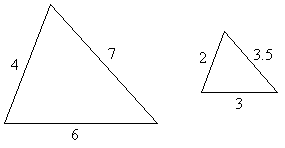
The remaining criteria prove similarity through proportionalities. One of these criteria is the side-side-side (proportionality) condition, which simply states that if the corresponding sides of two triangles are all proportional (that is, they share the same constant of proportionality), then they are similar triangles. Consider, for instance, the two triangles below.
Because each side of the rightmost triangle is half the length of the corresponding side in the leftmost triangle, the two triangles are therefore similar. As such, we can also conclude that the corresponding angles for the two triangles are congruent.
The last criterion for similarity that we will discuss is the side-angle-side (proportionality) condition. In this case, two triangles are similar if two corresponding sides are proportional and the included angles are congruent. Consider the two triangles below.
These two triangles are similar because the corresponding labeled sides are proportional (the length of the sides for the rightmost triangle are 5/3 times the lengths of the sides for the leftmost triangle) and the corresponding included angles are congruent. Thus, using any of the above criteria, we can prove that two triangles are congruent.
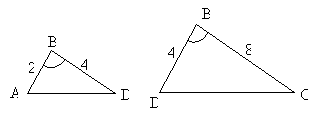
Practice Problem: Prove that triangles ABD and BCD are similar.
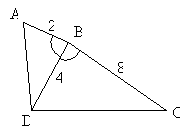

Solution: Let's prove that the triangles are similar using a two-column proof format. Note that the triangles have congruent angles 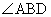 and
and 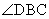 . We can also separate the triangles for clarity.
. We can also separate the triangles for clarity.

1. 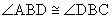 Given
Given
2. 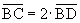 Given, 8 = 2 ∙ 4
Given, 8 = 2 ∙ 4
3. 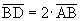 Given, 4 = 2 ∙ 2
Given, 4 = 2 ∙ 2
4. Sides BC and BD, and Statements 2 and 3
sides BD and AB are
proportional
5. Triangles ABD and BCD Side-angle-side (proportionality) condition
are similar
Thus, we have shown the two triangles to be similar.
Practice Problem: Prove that any two equilateral triangles are similar.
Solution: We know from our study of triangles that an equilateral triangle contains three congruent angles; thus, the measure of each angle in an equilateral triangle is 60°. As a result, by the angle-angle condition, all equilateral triangles must be similar to one another.
Practice Problem: Two isosceles triangles both have an interior angle of 100°. Prove that these triangles are similar.
Solution: Let's start by drawing a diagram (which is not necessarily to scale). We'll call the two isosceles triangles ABC and XYZ.


Because a triangle has only 180° total, the other two angles in each triangle must sum to 80°; furthermore, because the triangles are isosceles, these angles must be congruent to each other. Let's do a two-column proof to show our reasoning step by step.
1. 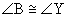 Given
Given
2. 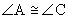 Isosceles triangle
Isosceles triangle
3. 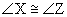 Isosceles triangle
Isosceles triangle
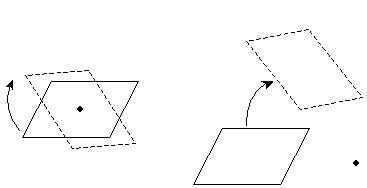
4. 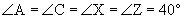 180° in a triangle
180° in a triangle
5. Triangles ABC and XYZ are Angle-angle condition
similar
More generally, we can say that any two isosceles triangles that have congruent obtuse angles must be similar. (The same reasoning applies-all that it required is that both isosceles triangles have an obtuse angle with the same measure.)
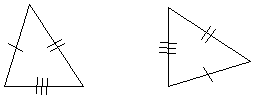




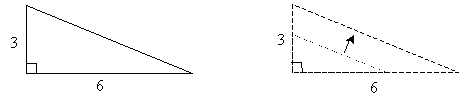




![]() and
and ![]() . We can also separate the triangles for clarity.
. We can also separate the triangles for clarity.

![]() Given
Given![]() Given, 8 = 2 ∙ 4
Given, 8 = 2 ∙ 4![]() Given, 4 = 2 ∙ 2
Given, 4 = 2 ∙ 2

![]() Given
Given![]() Isosceles triangle
Isosceles triangle![]() Isosceles triangle
Isosceles triangle![]() 180° in a triangle
180° in a triangle